
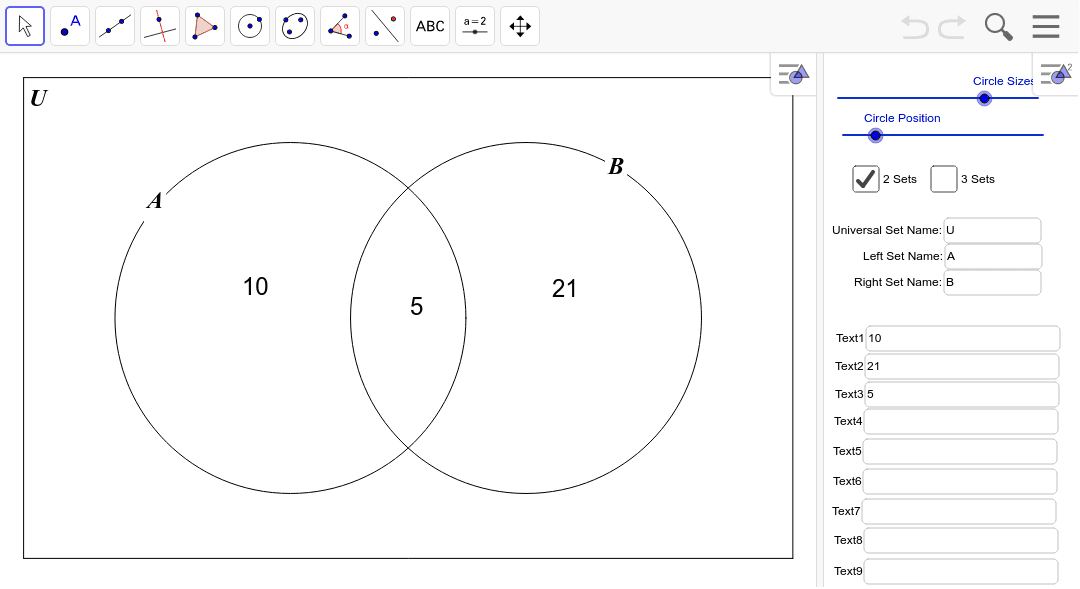
Number of students who like at least one of tea or coffee = n (only Tea) + n (only coffee) + n (both Tea & coffee) = 60 + 40 + 80 = 180Įxample 2: In a survey of 500 students of a college, it was found that 49% liked watching football, 53% liked watching hockey and 62% liked watching basketball.Number of students who like only one of tea or coffee = 60 + 40 = 100.Number of students who like neither tea nor coffee = 20.Number of students who like only coffee = 40.Number of students who like only tea = 60.Solution: The given information may be represented by the following Venn diagram, where T = tea and C = coffee. How many students like at least one of the beverages?.How many students like only one of tea or coffee?.How many students like neither tea nor coffee?.140 like tea, 120 like coffee and 80 like both tea and coffee. Solved ExamplesĮxample 1: In a college, 200 students are randomly selected. Tip: Always start filling values in the Venn diagram from the innermost value. Let M, C and P represent the courses Mathematics, Chemistry and Physics respectively.W = number of elements that belong to none of the sets A, B or C In a survey of university students, 64 had taken mathematics course, 94 had taken chemistry course, 58 had taken physics course, 28 had taken mathematics and physics, 26 had taken mathematics and chemistry, 22 had taken chemistry and physics course, and 14 had taken all the three courses. Total number of elements related to all the three sets A, B and C is Number of elements related to all the three sets A, B and C is Number of elements related only to (A and C) is Number of elements related only to (B and C) is Number of elements related only to (A and B) is We can get the following results from the Venn diagram shown above.


 0 kommentar(er)
0 kommentar(er)
